Four Fundamental Subspaces
Given a matrix \(A_{m \times n}\), there are 4 fundamental subspaces constructed from \(A\):
Column Space
Definition :
Column space \(C(A) \subseteq \mathbb{R}^m\) is a set of all linear combinations of column vectors in \(A\).
\(C(A) = \{\textbf{b}_{m\times 1} = A_{m \times n}\textbf{x}_{n \times 1} \mid \forall \textbf{x} \in \mathbb{R}^n\}\) Example:
Matrix \(A = \left[ \begin{matrix} 1 & 2 & 3 \\ 2 & 2 & 4 \\ 3 & 4 & 7 \\ \end{matrix} \right]\) has three column vectors \(\textbf{a}_1 = [1, 2, 3]^T\), \(\textbf{a}_2 = [2, 2, 4]^T\) and \(\textbf{a}_3 = [3, 4, 7]^T\) respectively.
Column space \(C(A)\) includes all vectors \(b\) such that
\[\textbf{b} = A \textbf{x} = \left[ \begin{matrix} \vert & \vert & \vert \\ \textbf{a}_1 & \textbf{a}_2 & \textbf{a}_3 \\ \vert & \vert & \vert \end{matrix}\right] \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix}\right] = x_1\left[\begin{matrix} \vert \\ \textbf{a}_1 \\ \vert \end{matrix} \right] + x_2\left[\begin{matrix} \vert \\ \textbf{a}_2 \\ \vert \end{matrix} \right] + x_3\left[\begin{matrix} \vert \\ \textbf{a}_3 \\ \vert \end{matrix} \right]\]with \(x_1, x_2, x_3 \in \mathbb{R}\).
Row Space
Definition :
Row space \(C(A^T) \subseteq \mathbb{R}^n\) is a set of all linear combinations of column vectors in \(A^T\).
Null Space
Definition :
Null space \(N(A) \subset \mathbb{R}^n\) is a set of vectors \(\textbf{x}_{n\times 1}\) such that \(A_{m\times n} \textbf{x}_{n\times 1} = \textbf{0}\).
\[N(A) = \{ \textbf{x}\mid A\textbf{x} = 0 \text{ and } \textbf{x} \in \mathbb{R}^n\}\]Similarly, null space \(N(A^T) \subset \mathbb{R}^m\) is a set of vectors \(\textbf{x}_{m\times 1}\) such that \(A^T_{n\times m} \textbf{x}_{m\times 1} = \textbf{0}\).
\[N(A^T) = \{ \textbf{x}\mid A^T\textbf{x} = 0 \text{ and } \textbf{x} \in \mathbb{R}^m\}\]Subspaces
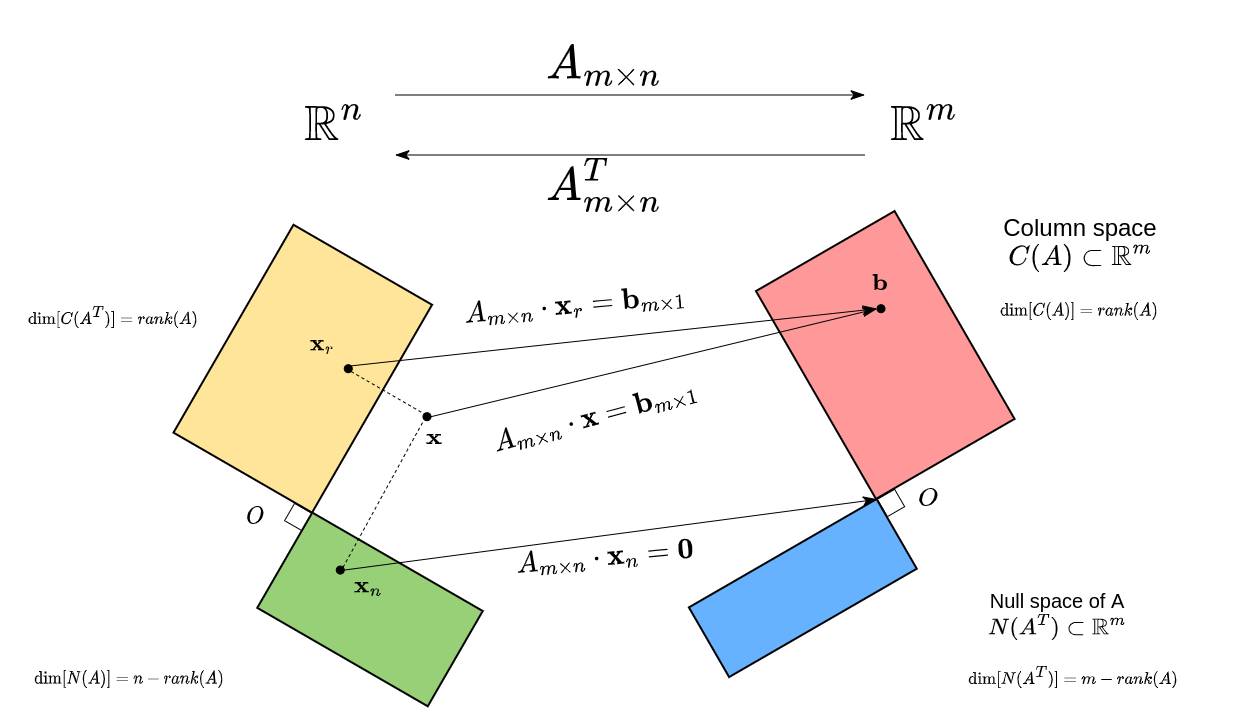
The reason \(C(A), C(A^T), N(A)\) and \(N(A^T)\) are called subspace is they are the subset of \(\mathbb{R}^m\) and \(\mathbb{R}^n\).
\[\operatorname{dim}C(A) = \operatorname{dim} C(A^T) = r = \operatorname{rank} A\] \[\operatorname{dim} N(A) = n - r\] \[\operatorname{dim} N(A^T) = m - r\]In the above figure, you can see the notation that \(C(A)\) and \(N(A^T)\) are perpendicular. The reason for it is:
\[\begin{aligned} A^T\textbf{x} &= \textbf{0} \\ \left[ \begin{matrix} - & \textbf{a}_1^T &- \\ - & \textbf{a}_2^T &- \\ &\vdots& \\ - & \textbf{a}_n^T &- \\ \end{matrix}\right] \textbf{x} & =\textbf{0} \end{aligned}\]which means \(\textbf{a}_i^T\textbf{x} = 0\) \(\rightarrow$ all\)\textbf{x}\(in\)N(A^T)\(is perpendicular with all column vectors of\)A$$.
\[\rightarrow N(A^T) \bot C(A)\]Transformation between subspaces
With an arbitrary \(\textbf{x}\), there is always a corresponding \(\textbf{b}\) in \(C(A)\) that:
\[A\textbf{x} = \textbf{b}\]We project \(\textbf{x}\) into 2 subspaces in \(C(A^T)\) and \(N(A)\):
\[\textbf{x}_r + \textbf{x}_n = \textbf{x}\]with \(\textbf{x}_r \in C(A^T)\) and \(\textbf{x}_n \in N(A)\).
Inserting \(\textbf{x}_r + \textbf{x}_n = \textbf{x}\) into \(A\textbf{x} = \textbf{b}\) and get:
\[\begin{aligned} A\textbf{x} &= \textbf{b} \\ A\textbf{x}_r + A\textbf{x}_n &= \textbf{b} \\ A\textbf{x}_r + \textbf{0} &= \textbf{b} \\ A\textbf{x}_r &= \textbf{b} \end{aligned}\]where \(\textbf{x}_r \in C(A^T)\) and \(\textbf{b} \in C(A)\).
So, we can conclude that matrix \(A\) transforms vectors in row space \(C(A^T)\) to column space \(C(A)\).