Singular Value Decomposition
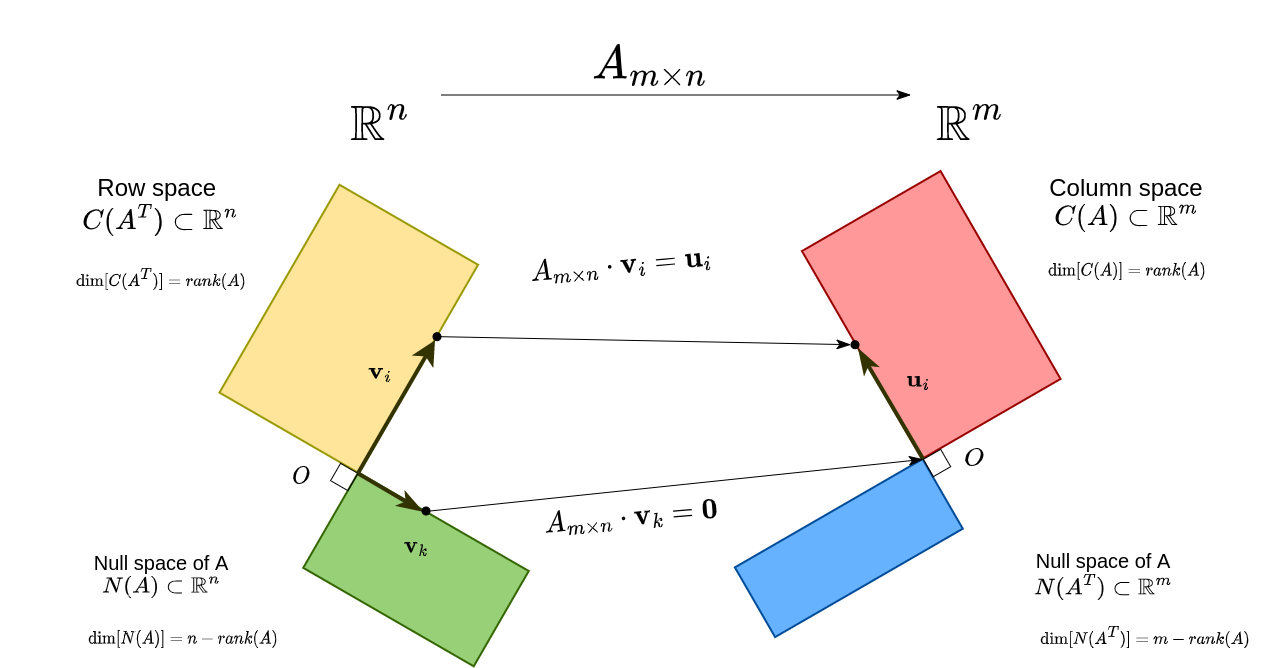
We already know that a matrix \(A_{m \times n}\) can transform a vector \(\textbf{x}_r \in C(A^T)\) into a vector \(\textbf{b} \in C(A)\). But these vectors \(\textbf{x}_r\) and \(\textbf{b}\) are just arbitrary vectors, so what if we want to transform axises of row space \(C(A^T)\) into axises of column space \(C(A)\)?
Vectors in a basics of a matrix is called axises if they are perpendicular and have unit length.
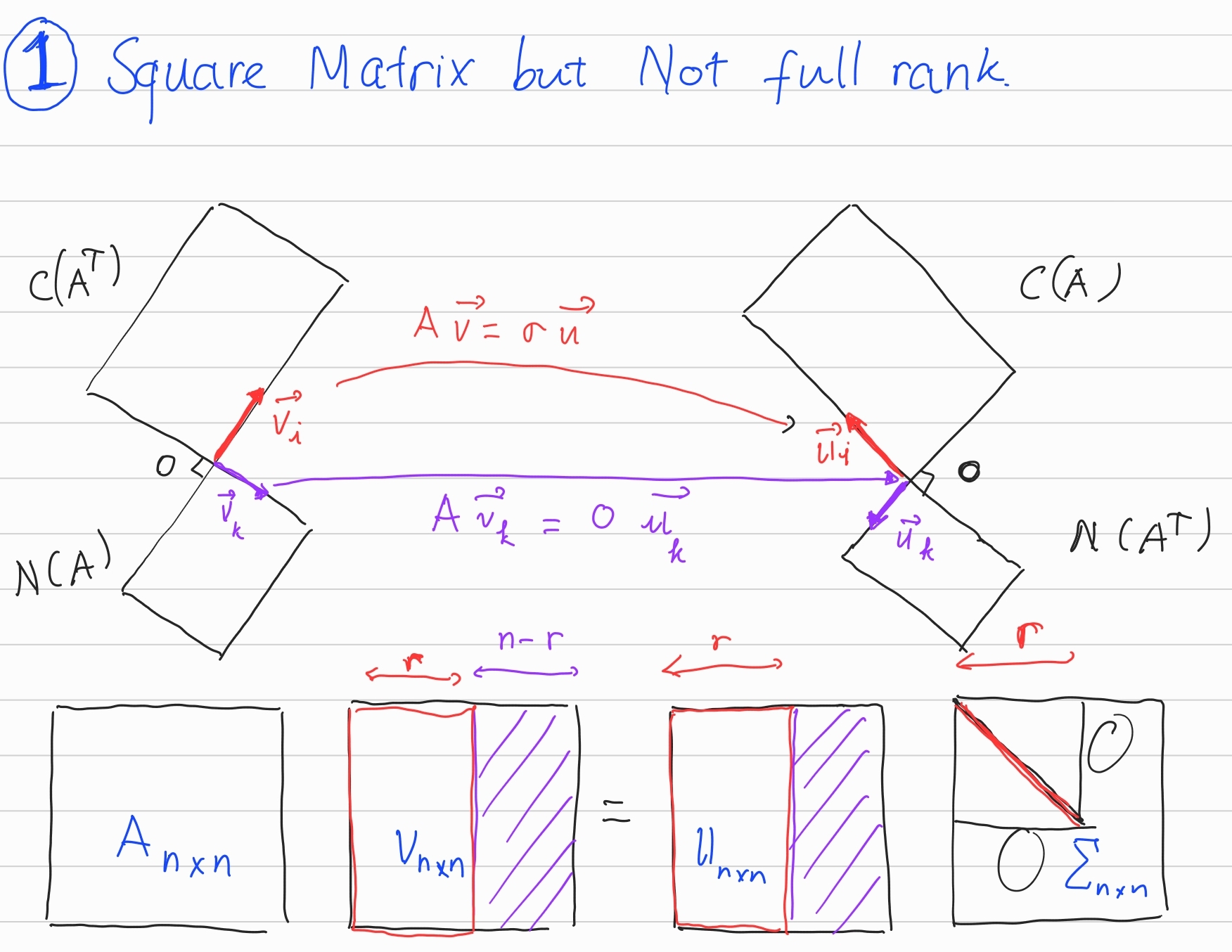
In case \(A\) is square matrix and full - rank.
Let:
- \(\{\textbf{v}_i\}\) be axises of row space \(C(A^T)\)
- \(\{\textbf{u}_i\}\) be axises of column space \(C(A)\)
Matrix \(A\) will transform each \(\textbf{v}_i\) to \(\textbf{u}_i\):
\[A\textbf{v}_i = \textbf{u}_i\]but this makes \(\textbf{u}_i\) and \(\textbf{v}_i\) maybe not unit, so be more accuracy, we put a scalar number \(\sigma_i\) for scaling \(\textbf{u}_i\).
\[A\textbf{v}_i = \sigma_i \textbf{u}_i\]We can compact all equations above and get:
\[\begin{aligned} A \left[ \begin{matrix} | & | & & | \\ \textbf{v}_1 & \textbf{v}_2 & \cdots & \textbf{v}_r \\ | & | & & | \\ \end{matrix}\right] &= \left[ \begin{matrix} | & | & & | \\ \textbf{u}_1 & \textbf{u}_2 & \cdots & \textbf{u}_r \\ | & | & & | \\ \end{matrix}\right] \left[ \begin{matrix} \sigma_1 & &\\ & \sigma_2 & \\ & & \ddots & \\ & & & \sigma_r \\ \end{matrix}\right] \\ A V &= U\Sigma \\ \Leftrightarrow A &= U \Sigma V^T \end{aligned}\]Since \(V\) is a set of axises of \(C(A^T)\), so \(V\) is an orthogonal matrix, \(VV^T = \mathbb{I}\).
In general case, we also want to transform axises of null space \(N(A)\) to that of \(N(A^T)\).
Since \(\textbf{v}_k\ \in N(A)\) is mapped to \(\textbf{0}\) after transformation, \(\sigma_k = 0\):
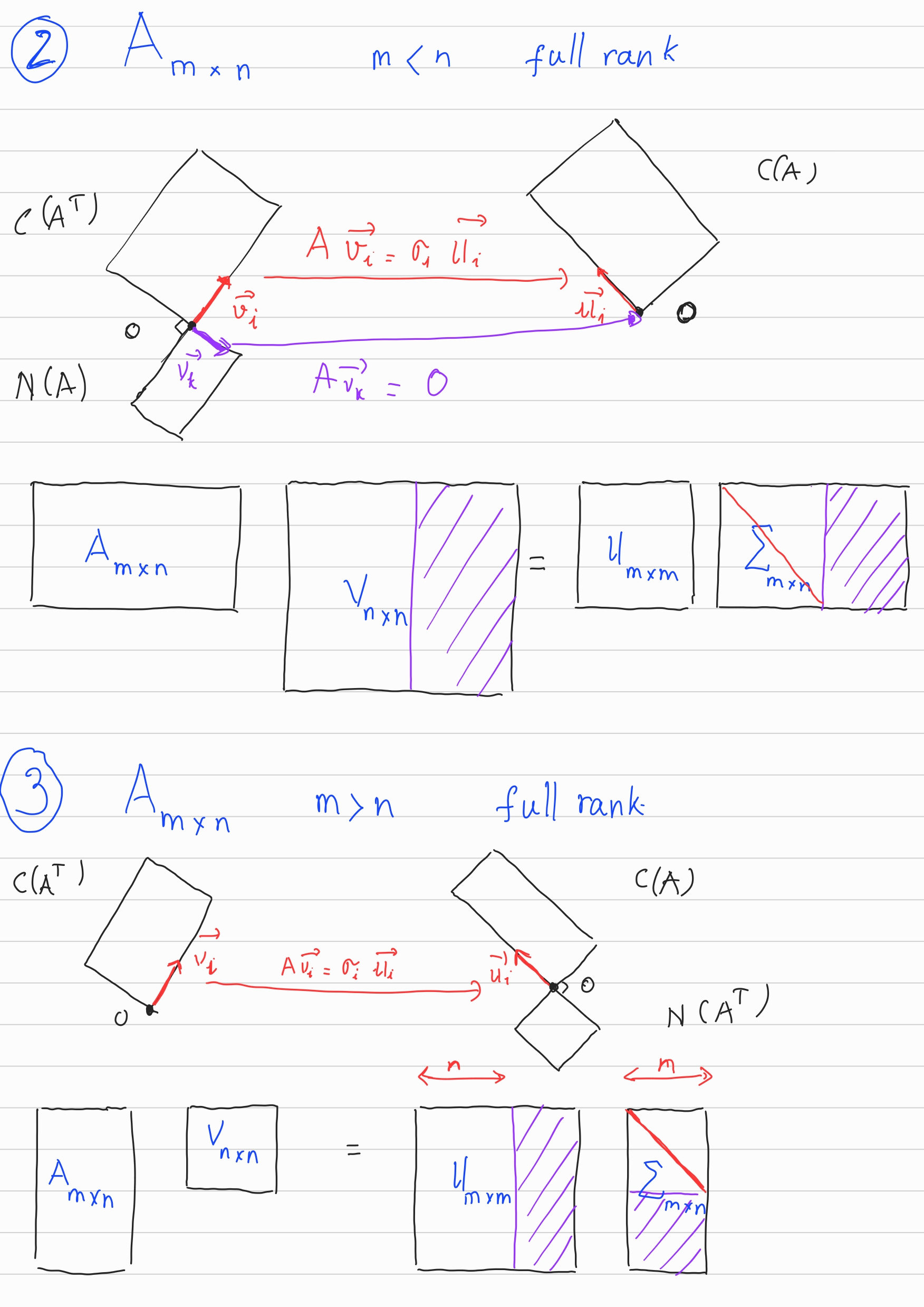
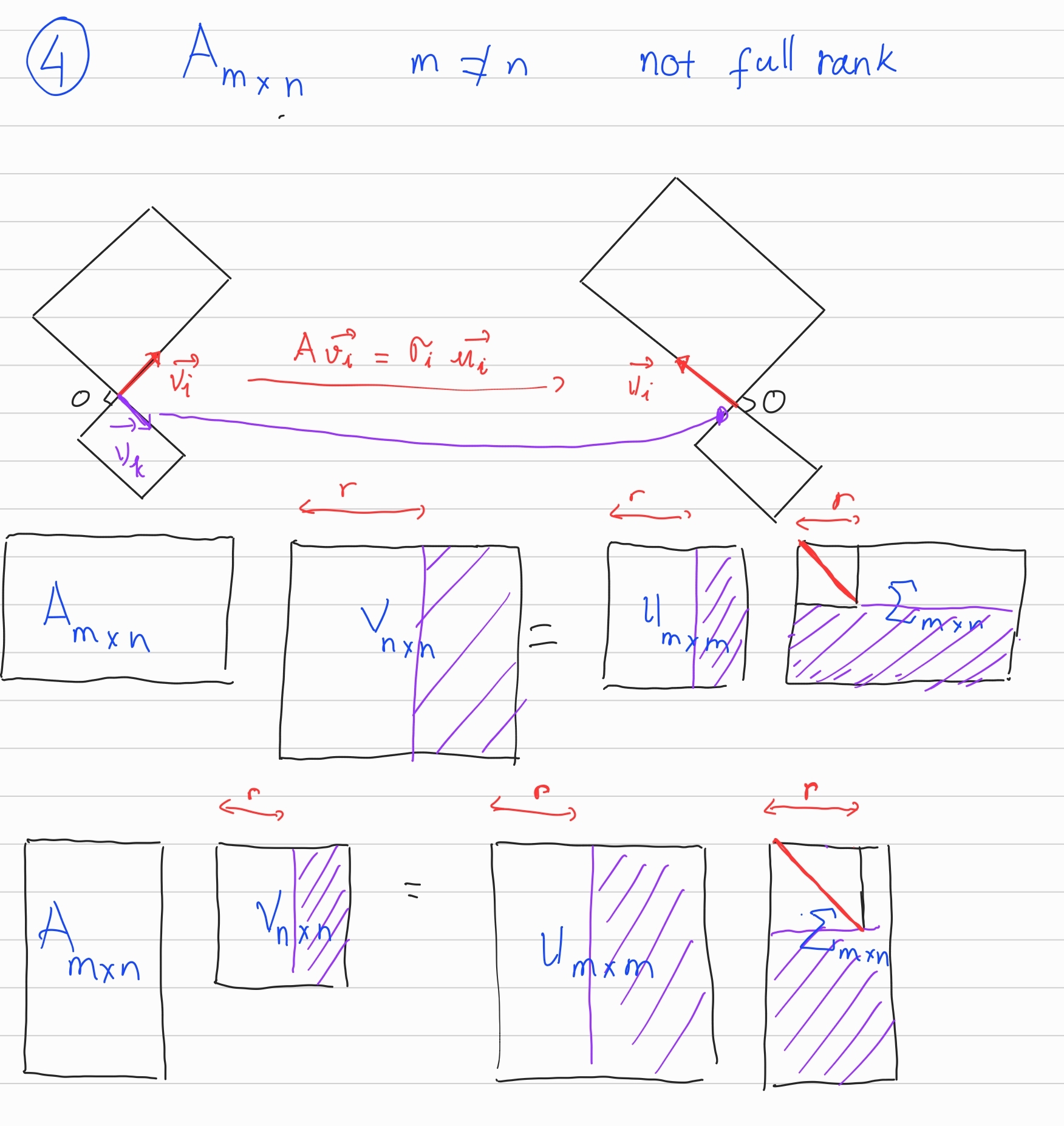
\[A\textbf{v}_k = 0 \textbf{u}_k\]Below are some possible cases when we do SVD for an arbitrary matrix.