Statistical Approaches to Level Set Segmentation
This blog will show you the general version of active contours model via statistical perspective and how to enhance the performance of this method.
Problem
Finding an optimal partition \(\mathcal{P}(\Omega)\) which segments an input image \(I\) can be seen as problem of maximizing a posteriori probability \(p(\mathcal{P}(\Omega)\mid I)\) and the Bayes’s rule for this conditional probability is:
\[p(\mathcal{P}(\Omega)\mid I) = \dfrac{p(I\mid \mathcal{P}(\Omega)) \, p(\mathcal{P}(\Omega))}{p(I)}.\]Since it is not easily to find \(p(I)\) of an input image so this term will be considered as constant.
The posteriori probability now is: \(p(\mathcal{P}(\Omega) \mid I) \propto p(I\mid \mathcal{P}(\Omega)) \, p(\mathcal{P}(\Omega)).\)
The prior \(p(\mathcal{P}(\Omega))\) is our prior knowledge about the partition to tackle with missing information. Usually, people choose the curve \(C\) having a length as short as possible:
\(p(\mathcal{P}(\Omega)) \propto e^{-\nu |C|}\) where \(\nu > 0\).
To specify the likelihood term \(p(I\mid\mathcal{P}(\Omega))\), we would make an assumption which is small regions of the partition \(\mathcal{P(\Omega)}\) are not overlapping, so the likelihood term can be expanded:
\[\begin{aligned} p(I \mid \mathcal{P}(\Omega)) &= p(I \mid \{\Omega_1, \Omega_2, \cdots, \Omega_n\}) \\ &= p( (I\mid \Omega_1) \cap (I\mid \Omega_2) \cap \cdots \cap (I\mid \Omega_n)) \\ &= \prod_{i = 1}^n p (I \mid \Omega_i) \end{aligned}\]Assume that each region \(\Omega_i\) has a feature function \(f_i(x, y)\) associating with each pixel location. This feature function can be a scalar value (e.g intensity of image), or a feature vector composing image gradients, color.
Another assumption that would be made is each pixel in each region is independent and identically distributed. The above expression can be read:
\[p(I \mid \mathcal{P}(\Omega)) = \prod_{i = 1}^n \prod_{(x, y) \in \Omega_i} p (f_i(x, y))^{dx \,dy}\]This assumption sometimes does not hold when we have image gradient in feature vector \(f\). Others argue that neighbor pixels are not i.i.d but actually have correlation due to similar intensities. However, at least, the assumption can give a chance to find an acceptable solution.
Finally, maximizing posteriori is equivalent to minimizing negative logarithm. The energy function will be:
\[E(\mathcal{P}(\Omega)) = -\sum_{i=1}^n\iint_{\Omega_i} \operatorname{log}(p(f_i(x, y))) \,dx \, dy - \nu |C|\]For simple cases, the distribution \(p(f_i(x, y))\) can be non parametric, but it can be also modeled as parametric distribution with parameter \(\theta\).
The complex version of the above energy function is:
\[E(\mathcal{P}(\Omega), \{\theta_i\}) = -\sum_{i=1}^n\iint_{\Omega_i} \operatorname{log}(p(f_i(x, y) \mid \theta_i)) \,dx \, dy - \nu |C|\]Binary Segmentation
In the binary segmentation problem, we try to find a partition separating foreground and background. If you already read this, you would be familiar with the below expansion.
We replace an unknown curve \(C: [0, 1] \rightarrow \Omega \subset \mathbb{R}^2\) by an unknown surface \(\phi: \Omega \subset \mathbb{R}^2 \rightarrow \mathbb{R}\). The curve \(C\), region inside \(C\): \(\Omega_1\) and outside \(C\): \(\Omega_2\) can be re - defined:
\[\begin{equation*} \begin{cases} C &= \{(x, y) \in \Omega \, | \, \phi(x, y) = 0\} \\ inside (C) &= \{(x, y) \in \Omega \, | \, \phi(x, y) > 0\} \\ outside (C) &= \{(x, y) \in \Omega \, | \, \phi(x, y) < 0\} \end{cases} \end{equation*}\]With the introduction of heaviside step function \(H(.)\), we can re - write the energy function:
- The first term:
- The second term:
- The energy function:
where \(\begin{equation*} H(x) = \begin{cases} 1 & \quad x \ge 0, \\ 0 & \quad x \lt 0. \end{cases} \end{equation*}\)
Solutions
Again, the method solving this problem is Euler - Lagrange Equation and gradient decent. We recommend you read this to familiarize yourself with the way we expand formulation.
\[E(\phi, \theta_1, \theta_2) = \underset{\Omega}{\iint} L(\phi, \nabla \phi, \theta_1, \theta_2) \, dx \, dy\]The optimal \(\phi\), \(\theta_1\) and \(\theta_2\) are:
\[\begin{aligned} \underset{\phi, \theta_1, \theta_2}{\operatorname{arg\,min}} \, E(\phi, \theta_1, \theta_2) = \underset{\Omega}{\iint} L(\phi, \nabla \phi, \theta_1, \theta_2) \, dx \, dy \end{aligned}\]To solve this, first we would iteratively find optimal values/ function of each \(\theta_1\), \(\theta_2\) and \(\phi\):
-
Step 1: Considering \(\phi\) and \(\theta_2\) as constants, the optimal value of \(\theta_1\) is: \(\theta_1 = \underset{\theta_1}{\operatorname{arg\,min}} \, \iint_{\Omega} H(\phi(x, y)) \operatorname{log}(p(f_1(x, y)| \theta_1)) \, dx \, dy\)
-
Step 2: Considering \(\phi\) and \(\theta_1\) as constants, the optimal value of \(\theta_2\) is: \(\theta_2 = \underset{\theta_2}{\operatorname{arg\,min}} \, \iint_{\Omega} H(\phi(x, y)) \operatorname{log}(p(f_2(x, y)| \theta_2)) \, dx \, dy\)
-
Step 3: Considering \(\theta_1\) and \(\theta_2\) as constants, update step of \(\phi\) is: \(\dfrac{\partial \phi}{\partial t} = - \dfrac{dE}{d\phi} = \delta(\phi) \left( \nu \operatorname{div} \left(\dfrac{\nabla \phi}{|\nabla \phi|} \right) + \operatorname{log} \dfrac{p(f_1|\theta_1)}{p(f_2|\theta_2)} \right)\)
In implementation, rather having heaviside step and dirac delta function as discrete functions, we replace them by their softer versions:
\[\begin{aligned} H(x) &= \dfrac{1}{2}\left( 1 + \dfrac{2}{\pi} \operatorname{arctan}\left( \dfrac{x}{\epsilon}\right)\right) \\ \delta(x) &= \dfrac{\epsilon^2}{\pi(\epsilon^2 + x^2)} \end{aligned}\]where \(\epsilon = 10^{-6}.\)
Grey Scale Images
In some cases and for the sake of simplicity (also running time), we can assume that feature vector \(f\) is intensity, the distribution \(p(f_i \mid \theta_i)\) is Gaussian:
\[p(f_i|\theta) = p(I|\mu_i, \sigma_i) = \dfrac{1}{\sqrt{2\pi\sigma_i^2}}\operatorname{exp}\{-\dfrac{(I - \mu_i)^2}{2\sigma_i^2}\}.\]The update equations for \(\mu_i, \theta_i\) and \(\phi\) will be:
\[\begin{aligned} \mu_1 &= \dfrac{\underset{\Omega}{\iint} H(\phi (x, y)) I(x, y) \, dx \, dy}{\underset{\Omega}{\iint} H(\phi (x, y)) \, dx \, dy} \\ \sigma_1 &= \dfrac{\underset{\Omega}{\iint} H(\phi (x, y)) (I(x, y) - \mu_1)\, dx \, dy}{\underset{\Omega}{\iint} H(\phi (x, y)) \, dx \, dy} \\ \mu_2 &= \dfrac{\underset{\Omega}{\iint} (1 - H(\phi (x, y))) I(x, y) \, dx \, dy}{\underset{\Omega}{\iint} (1 - H(\phi (x, y))) \, dx \, dy} \\ \sigma_2 &= \dfrac{\underset{\Omega}{\iint} (1 - H(\phi (x, y))) (I(x, y) - \mu_2)\, dx \, dy}{\underset{\Omega}{\iint} (1 - H(\phi (x, y)))\, dx \, dy} \\ \dfrac{\partial \phi}{\partial t} &= \delta(\phi)\left(\nu \operatorname{div}\left(\dfrac{\nabla \phi}{|\nabla \phi|}\right) + \dfrac{(I - \mu_2)^2}{2\sigma_2^2} - \dfrac{(I - \mu_1)^2}{2\sigma_1^2} + \operatorname{log}\dfrac{\sigma_1}{\sigma_2}\right) \end{aligned}\]Have you seen the similarity of this and that of previous? :)
Vector - valued Images
Our assumption for feature vector \(f_i\) can also be color vector \(f = \left<R, G, B\right>\) or based on the structure of image \(f = \left<I, \dfrac{I_x}{\vert\nabla I\vert}, \dfrac{I_y}{\vert\nabla I\vert}, \dfrac{2I_xI_y}{\vert\nabla I\vert}\right>\).
The update equation for \(\mu_i\) and \(\Sigma_i\) will be:
\[\begin{aligned} \mu_i &= \dfrac{1}{|\Omega_i|}\underset{\Omega_i}{\iint} H(\phi (x, y)) I(x, y) \, dx \, dy \\ \sigma_i &= \dfrac{1}{|\Omega_i|}\underset{\Omega_i}{\iint} H(\phi (x, y)) (I(x, y) - \mu_i) \, (I(x, y) - \mu_i)^T\, dx \, dy \end{aligned}\]Results
The distribution we used in the daisy samples is Single Variable Gaussian Distribution.
| Results | Results |
|---|---|
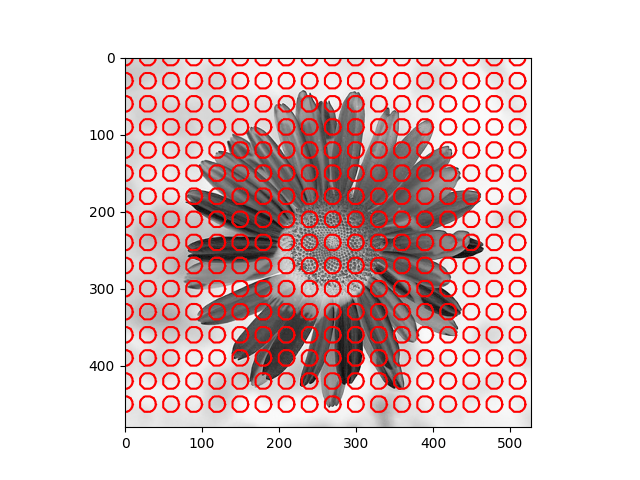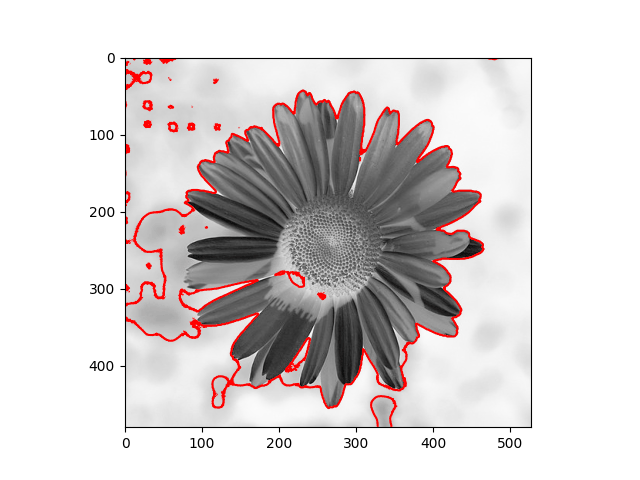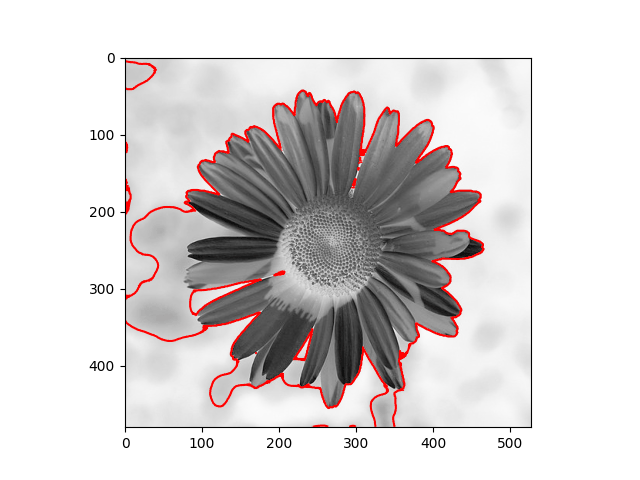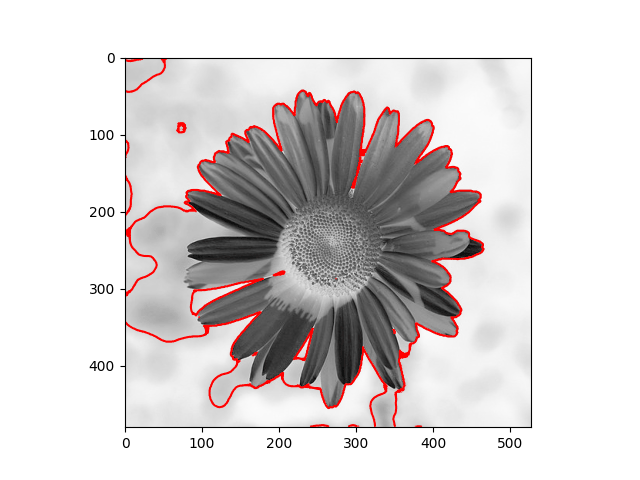 |
 |
Reference
[1] CREMERS, Daniel; ROUSSON, Mikael; DERICHE, Rachid. A review of statistical approaches to level set segmentation: integrating color, texture, motion and shape. International journal of computer vision, 2007, 72.2: 195-215.